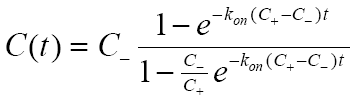Mathematical Models Implemented in CURFIT

The following fitting models are implemented in CURFIT:

• Sum of exponents. The maximal number of exponential terms is 4. In addition to the amplitudes ( F(i) ) and the kinetic constants ( k(i) ), the equation also contains the "Limit" parameter. Its implemented form is:

where Y_i  and X_i are the abscissa and ordinate of the i-th point and N is the number of exponents.

• Polynomial. The maximal order is 10.

• Michaelis-Menten equation. It is implemented in the following form:

  

• Sum of 2 Michaelis-Menten equations:

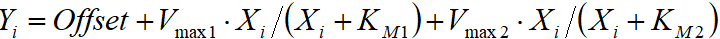
• Hill equation:

• Ligand binding. It is an equation for the dependence of equilibrium of binary association (e.g., enzyme-substrate or receptor-ligand interactions) on the concentration of the interacting species. This equation is also called the "tight binding equation" or "square root" equation. It is implemented in SpectraLab in four different variants for the following cases:

1.  Titration. It is the most common case, which is applicable to titration of an enzyme (receptor) with a ligand. The abscissa value (Y_i) is presumed proportional to the concentration of the complex (with a possible offset). The ordinate values (X_i) correspond to the ligand concentration. The concentration of the enzyme (Z) is taken from the Z-value associated with the trace (thus, before fitting the trace, the user must place the enzyme concentration into the Z-column of the SpectraLab datasheet). The equation also includes the Limit and A_max parameters, which correspond to the level of the signal at an infinite concentration of the ligand, and the maximal amplitude of the changes (i.e., the limit minus the signal at no ligand present), respectively:

2. Dilution. This is the case of "titration by dilution", where the ratio of the concentrations of interacting species is kept constant, but their total concentration is changing (i.e., their mixture is diluted stepwise). In this case, the Z-value associated with the trace should be set to the ratio of the concentration of ligand to that of the enzyme, and the ordinate values (X_i) should contain the enzyme concentrations. In this case, the equation has the following form. The Y_i values should be normalized proportionally to dilution prior to fitting:

3. Dimerization. This is an equation for the position of equilibrium of protein dimerization. Z-value is not used in this case. The ordinate values correspond to the protein concentration:

4. Job's titration. This is the case of Job's titration experiment, where the total concentration of the interacting compounds remains constant but their ratio changes. In this case, the Z-value should be set to the total concentration of the reagents, and the ordinate values correspond to the molar fraction of the ligand (should be within the 0 to 1 range):

• Infinite cooperativity binding. This is the case of simultaneous binding of a ligand (S) to n binding centers in a protein (E) with the formation of the complex ES_n. The number of binding centers can be varied from 1 to 10. The concentration of the complex ES_n is calculated by solving (numerically) the following equation relative to [ES_n]:
  

where [E]₀ and [S]₀ are the total concentration of enzyme and substrate, respectively. The ordinate values (X_i) correspond to the ligand concentration. The сoncentration of the enzyme is taken from the Z-value associated with the trace. In the case of n=1, this model is similar to that of the tight-binding equation (see "Ligand binding" case above). The abscissa values (Y_i) are presumed proportional to the concentration of the complex ES_n with a possible offset: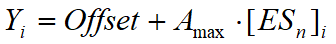 

This model is realized in three variants: for the ordinary titration case, for Job's titration in its regular setup, and for Job's titration in its "counterflow" (tandem cell) setup (see Davydov et al., 2006 for more details).

• 2-nd order kinetics. This model is for the kinetics of product formation in an irreversible bimolecular reaction, A + B→C.  The abscissa value (Y_i) is presumed proportional to the concentration of the product (C) with a possible offset. The ordinate values (X_i) correspond to the time coordinate. When selecting this model, the user will be asked for the ratio of reagents (r=[A]₀/[B]₀).  The ratio is expected to be greater or equal to unity  (r≥1) so that the lowest of the two concentrations is taken as the base. The values from 1.0 to 10⁹ are allowable.  As it is known from the chemical kinetic textbooks, the second-order kinetics equations for r=1 and r≠1 differ.  They are implemented in SpectraLab in the following forms:

1.  r=1:                       
2. r>1:                         

In these equations, k_I is the second-order rate constant multiplied by the lesser of the concentrations of the two compounds. Thus, to obtain the second-order rate constant from this parameter (which is labeled "k[A0]" in the fitting output), one should divide it by the lesser of the initial concentrations of the interacting compounds (or any of them if r=1). 

• Kinetics of reversible second-order reaction. This model is for the kinetics of reversible association of two compounds,  A + B↔C.  It is applicable to the kinetics of the formation of enzyme-substrate or receptor-ligand complexes, even at comparable concentrations of interacting compounds. Here again, the abscissa value (Y_i) is presumed proportional to the concentration of the product (C), and the ordinate corresponds to the time coordinate. The kinetic equation for this case may be found in the "Kinetic methods in biochemical research" book by Varfolomeev and Zaitsev (page 183, equations 8.22 - 8.24). In a slightly different form, it is published in Lehnert and Figge, 2017 (equation 11), although the expression found in this article contains a typo (there should be C₊ instead of C_- in the denominator). Kinetic model for this case implemented in SpectraLab is based on the following relationship that determines the time course of the changes in the concentration of product ( C(t) ):

where  ,  , and A₀ and B₀ correspond to the initial concentrations of the interacting species. The ordinate values (X_i) correspond to the ligand concentration. The abscissa values (Y_i) are presumed proportional to the concentration of the product of association with a possible offset:

 

When selecting this model, the user will be asked for the molar ratio of the ligand to the enzyme. The values from 10^-9 to 10⁹ are allowed for this parameter.  Z-value associated with the trace should be set to the initial concentration of the enzyme before fitting to this model.

•  Arrhenius equation for the temperature dependence of the kinetic constant of a chemical reaction:

The ordinate values (X_i) should be set to temperature on the Celsius scale. The abscissa values (Y_i) are presumed proportional to the reaction rate. The parameters estimated by the fitting are the pre-exponential factor (A) and the energy of activation (E_a), which is given in kJ/mol units. 

• Pressure dependence of equilibrium. This model is for pressure dependence of the position of equilibrium in a reversible first-order transition, A ↔ B, characterized with the pressure-dependent constant of equilibrium, K_eq=[A]/[B]. As described in "Protein interactions" book by Gregory Weber (p. 212, Eq. 9), when expressed relative to the molar fraction of compound A at pressure P (A_p), this dependence obeys the following relationship:
  

where ΔV° is the molar volume change in the transition,  P_½ is the pressure at which K_eq=1 and K°_eq is the value of K_eq extrapolated to zero: . The form of this relationship implemented in SpectraLab is:

 

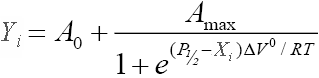
The ordinate values (X_i) correspond to hydrostatic pressure. The abscissa values (Y_i) are presumed to be equal to a sum of a value proportional to the molar fraction of compound A (A_p),  and a possible offset (A₀). Z-value associated with the trace should be set to temperature expressed on Celsius scale. If Z-vale is not set, 25 °C temperature is assumed by default. If X_i is expressed in bars, P_½ and ΔV° values resulting from the fitting are expressed in bars and ml/mol, respectively. If ΔV° is negative, increasing pressure displaces the equilibrium towards compound A. Otherwise, it is displaced towards B.

• Trimerization equilibrium. This model describes the concentrational dependence of reversible trimerization of a compound, 3A ↔ A₃, in which the equilibrium is determined by the dissociation constant K_D.  Ordinate corresponds to the total concentration of the protein, and the abscissa is presumed proportional to the concentration of trimers with a possible offset. Z-value is not used. The underlying mathematical equations may be found in Davydov et al., 2015.

• Combination of the Hill and substrate inhibition equations. This model is described in Muller et al, 2015. Ordinate corresponds to the substrate concentration and the abscissa is presumed proportional to the enzymatic activity with a possible offset. Z-value is not used.

• Two-site binding of a ligand. This is the case of parallel or sequential models of binding of a ligand (S) to two binding sites of a protein (E) described in Fernando et. al, 2006 and Fernando et.al., 2011. The observed signal is presumed to reflect the formation of both binary (SE) and ternary (SES) complexes, where the ratio of the amplitudes of the signal from SE to the total of those from SES and SE is determined by the parameter F(SE). Thus, at F(SE)=0.5, the formation of both types of complexes results in the signal of the same amplitude. This model also allows the observed signal (Y_i) to include a constant offset. Similar to the "Ligand binding" model, this offset is determined by the combination of the Limit and A_max parameters. X-coordinate corresponds to the concentration of the ligand. Z-value associated with the trace should be set at the concentration of the protein. Upon selecting this model, the user will be asked to select between the Parallel and Sequential binding sub-models. The underlying mathematical equations may be found in Fernando et. al, 2006 and Fernando et.al., 2011.

• Two-site binding of a ligand, Job's titration case. This is the same model as above but realized for the case of Job's (continuous variation) titration in its traditional ("Bell") and "counterflow" ("Tandem", Davydov et al., 2006) implementations. In this case, the Z-value should be set to the total concentration of the interacting species, and the ordina (X_i) should correspond to the molar fraction of the ligand at each point of the titration.